Физическая природа звука
Звук является спутником человека в течение всей его жизни, но мало кто задумывается, что он собой представляет. С физической точки зрения звук можно определить как колебательные движения частиц в упругой среде, вызванные каким-либо источником, коротко — упругие волны. Скорость звука зависит от свойств среды, в которой он распространяется: в газах скорость звука растет с ростом температуры и давления, в жидкостях при росте температуры наоборот снижается (исключением является вода, в которой скорость звука достигает максимума при 74°С и начинает снижаться только при увеличении данной температуры). Для воздуха такая зависимость выглядит так:
С = 332 + 0,6tc
где tc — температура окружающей среды, °С.
Таблица 1. Скорость звука в газах, при температуре 0 °С и давление 1 атм.
| Азот | 334 м/с |
| Кислород | 316 м/с |
| Воздух | 332 м/с |
| Гелий | 965 м/с |
| Водород | 1284 м/с |
| Метан | 430 м/с |
| Аммиак | 415 м/с |
Таблица 2. Скорость звука в жидкостях при температуре 20 °С.
| Вода | 1490 м/с |
| Бензол | 1324 м/с |
| Спирт этиловый | 1180 м/с |
| Ртуть | 1453 м/с |
| Глицерин | 1923 м/с |
В твердых телах скорость звука определяется модулем упругости вещества и его плотностью, при этом в продольном и поперечном направлении в неограниченных изотропных твердых телах она различается.
Таблица 3. Скорость звука в твердом теле.
| Вид твердого тела | Скорость продольной волны, м/с | Скорость поперечной волны, м/с |
|---|---|---|
| Плавленый кварц | 5970 | 3762 |
| Бетон | 4200–5300 | — |
| Плексиглас | 2675 | 1110 |
| Стекло | 3760–4800 | 2380–2560 |
| Тефлон | 1340 | — |
| Полистирол | 2350 | 1120 |
| Сталь | 5740 | 3092 |
| Золото | 3220 | 1200 |
| Мрамор | 3810 | — |
| Алюминий | 6400 | 3130 |
| Полиэтилен | 2000 | — |
| Серебро | 3650–3700 | 1600–1690 |
| Дуб | 4100 | — |
| Сосна | 3600 | — |
Из таблиц наглядно видно, что скорость звука в газах значительно ниже, чем в твердых телах, именно поэтому в приключенческих фильмах часто можно увидеть, как люди прикладывают ухо к земле, чтобы определить наличие погони за собой, также это явление заметно рядом с железной дорогой, когда звук приходящего поезда, слышится дважды — в первый раз он передается по рельсам, а второй — по воздуху.
Процесс колебательного движения звуковой волны в упругой среде, можно описать на примере колебания частицы воздуха:
— на частицу воздуха, вынужденную сдвинуться со своей начальной позиции, из-за воздействия источника звука, действуют упругие силы воздуха, которые пытаются вернуть ее на свое первоначальное место, но из-за действия сил инерции, возвращаясь, частица не останавливается, а начинает удаляться от начальной позиции в противоположную сторону, где в свою очередь на нее также действуют упругие силы и процесс повторяется.
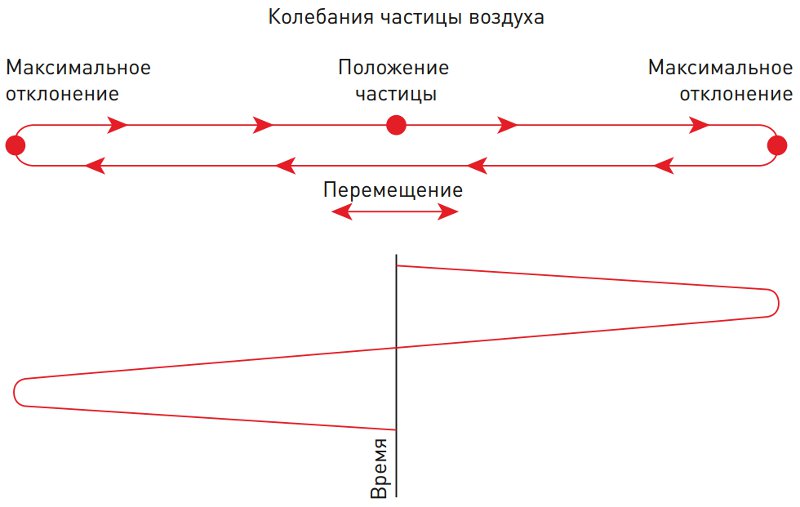
Рисунок 1. Процесс колебания частицы воздуха
На рисунке (рисунок №2) маленькими точками образно представлены молекулы воздуха (в кубометре воздуха их более миллиона). Давление в области компрессии несколько превышает атмосферное, а в области разрежения, наоборот, — ниже атмосферного. Направление малых стрелочек показывает, что, в среднем, молекулы движутся направо из области высокого давления и налево из области низкого. Любая из представленных молекул сначала проходит определенное расстояние в правую сторону, а затем такое же расстояние в левую, относительно своей первоначальной позиции, в то время как звуковая волна двигается равномерно в правую сторону.
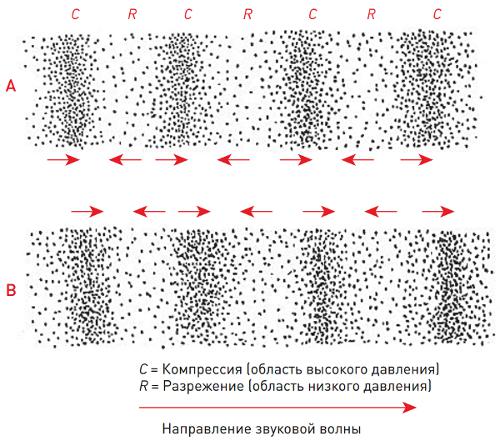
Рисунок 2. Перемещение звуковой волны
Логично задать вопрос — почему звуковая волна перемещается вправо? Ответ можно найти при внимательном рассмотрении стрелочек на предыдущем рисунке: в месте, где стрелочки сталкиваются с друг другом образуется новое скопление молекул, которое будет находится с правой стороны от первоначальной области компрессии, при удалении от места столкновения стрелочек плотность молекул снижается и образуется новая область разрежения, следовательно постепенное перемещение области высокого и низкого давления приводит к движению звуковой волны в правую сторону.
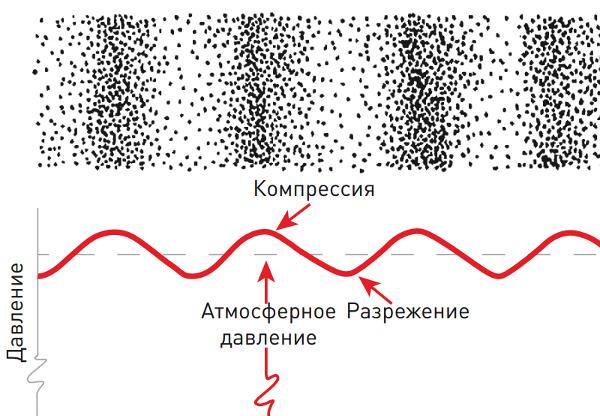
Рисунок 3. Процесс перемещения звуковой волны
Волновое движение такого рода называется гармоническими или синусоидальными колебаниями, которое описывается следующим образом:
x(t) = Asin(wt + φ)
Простая гармоническая или синусоидальная волна изображена на рисунке (Рисунок №4):
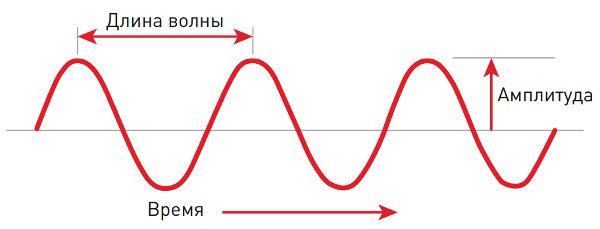
Рисунок 4. Синусоидальная волна
Длина волны зависит от частоты и скорости звука:
Длина волны (м) = Скорость волны (м/с) / Частота (Гц)
Cоответственно частота определяется следующим образом:
Частота (Гц) = Скорость волны (м/с) / Длина волны (м)
Из этих уравнений видно, что с увеличением частоты — длина волны уменьшается.
Таблица 4. Длина волны в зависимости от частоты звука (при температуре воздуха 20 °С)
| Частота, Гц | 31,5 | 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | 16000 |
| Длина волны, м | 10,9 | 5,44 | 2,74 | 1,37 | 0,69 | 0,34 | 0,17 | 0,084 | 0,043 | 0,021 |
Интенсивность звука снижается по мере увеличения расстояния от источника звука. Если звуковая волна на своем пути не встречает преград, то звук из источника распространяется во всех направлениях. На рисунке (рисунок №5) изображен характер изменения интенсивности звука — сила звука остается постоянной, но площадь воздействия увеличивается, именно поэтому в отдельно взятой точке интенсивность звука снижается.
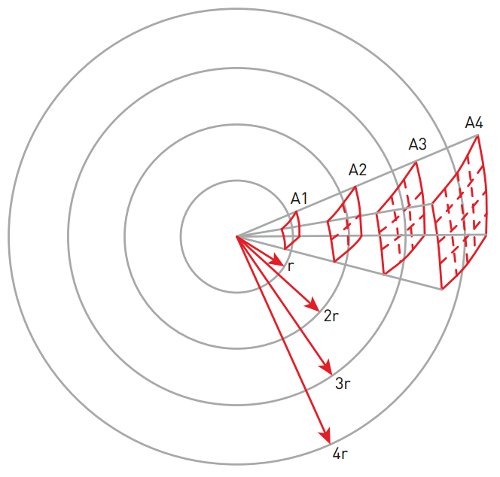
Рисунок 5. Процесс распространения звуковой волны
В зависимости от вида источника звука — существует несколько видов звуковых волн: плоские, сферические и цилиндрические.
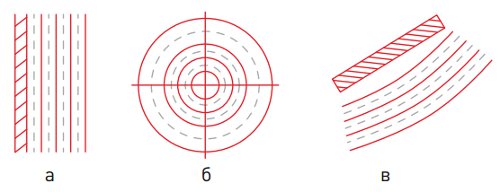
Рисунок 6. Виды источников звука и схематическое изображение фронта волны
а — протяженная пластина; б — точечный источник; в — линейный источник.
Плоские волны при распространении не меняют форму и амплитуду, сферические не меняют форму (амплитуда уменьшается как 1/r), цилиндрические меняют и форму, и амплитуду (убывает как 1/r