Количественная мера звука — различия между версиями
Admin (обсуждение | вклад) |
Admin (обсуждение | вклад) |
||
| Строка 120: | Строка 120: | ||
| Частотная характеристика "А" шумомера, дБ || 30,2 || 26,2 || 22,5 || 19,1 || 16,1 || 13,4 || 10,9 || 8,6 || 6,6 || 4,8 || 3,2 || 1,9 || 0,8 || 0 || 0,6 || 1 || 1,2 || 1,3 || 1,2 || 1 || 0,5 | | Частотная характеристика "А" шумомера, дБ || 30,2 || 26,2 || 22,5 || 19,1 || 16,1 || 13,4 || 10,9 || 8,6 || 6,6 || 4,8 || 3,2 || 1,9 || 0,8 || 0 || 0,6 || 1 || 1,2 || 1,3 || 1,2 || 1 || 0,5 | ||
|} | |} | ||
| + | |||
| + | [[Категория:Словарь]] | ||
Текущая версия на 17:14, 8 августа 2013
Звуковое давление, соответствующее нулевому порогу слышимости человеческого уха на частоте 1000 Гц, равно 2х10–5 Па, а максимальное значение звукового давления, которое воспринимает ухо, равно 2х103 Па, то есть минимальное и максимальное значение звукового давления отличаются в 100 000 000 раз!
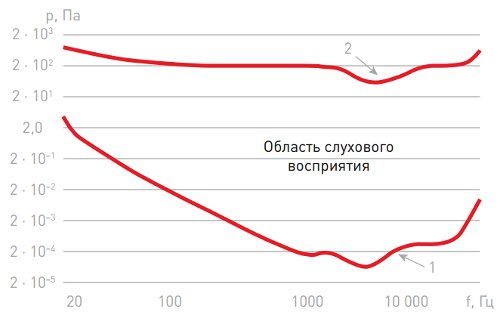
Рисунок 1. Область слухового восприятия человека
1 — порог слышимости, 2 — болевой порог
Легко представить, что математические действия с числами такого порядка будут весьма затруднительны, поэтому основной мерой звука в акустике является децибел (дБ) (отношение двух одноименных физических величин). Для определения уровней звукового давления и уровня звука используется следующая формула:
L = 20 * lg (p/p0), дБ
где: p - среднеквадратичное значение звукового давления, измеряемое в паскалях; p0 - нулевой порог слышимости (2х10-5 Па);
Система измерения звука в децибелах, позволяет легко сравнивать величины звука соизмеримые с чувствительностью человеческого уха, не используя для этого числа с большим количеством нулей. Область восприятия звука человеком в шкале децибел от 0 дБ (нулевой порог) до 130–140 дБ (болевой порог).
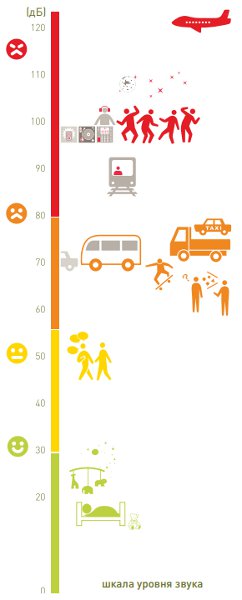
Рисунок 2. Типичные источники звука, измеренные в децибелах
Для акустических расчетов достаточно часто используются такие характеристики, как уровни интенсивности и уровни звуковой мощности, которые определяются по формулам:
L = 10 * lg (I/I0), дБ L = 10 * lg (W/W0), дБ
где: I и W - среднеквадратичные значения интенсивности и мощности звука; I0 = 10–12 Вт/м2;W0 = 10–12 ≈ Вт — значения нулевых порогов соответственно интенсивности и мощности звука.
Математические действия с децибелами:
Так, как децибел логарифмическая величина, то арифметические действия с ними имеют свои особенности, например:
L1 + L2 = 60дБ + 60дБ = 10 lg (100,1*60 + 100,1*60) = 10 lg (106 + 106) = 10 lg (2 * 106) = 10 * 6,3 = 63дБ
а:
L1 + L2 = 60дБ + 70дБ = 10 lg (100,1*60 + 100,1*70) = 10 lg (106 + 107) = 10 lg (11 * 106) = 10 * 7,04 = 70дБ
Формула сложения децибел имеет вид:
L1 + L2 = 10 lg (100,1L1 + 100,1L2)
Удобно для расчетов использовать следующую таблицу:
Таблица 1. Операции с Уровнями Звукового Давления (УЗД)
| Разность УЗД (УЗ) двух складываемых источников дБ (дБА) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Добавка (Δ) к большему УЗД (УЗ), дБ (дБА) | 3 | 2,5 | 2,1 | 1,8 | 1,5 | 1,2 | 1,0 | 0,8 | 0,6 | 0,5 | 0,4 |
В реальных условиях создать звук строго определенной частоты могут только специальные приборы — зависимость уровней звукового давления от частоты называют спектром звука. В зависимости от частоты человеческое ухо по-разному воспринимает звук: на высоких частотах звук воспринимается лучше, чем на низких .Поэтому болевой порог на низких частотах выше, чем на высоких. Именно поэтому необходимо знать частотную характеристику звука, которая показывает уровни звука в зависимости от его частоты. В акустике используют восемь диапазонов частот, называемых октавными полосами частот, в составе каждой из которых выделяют три частотных диапазона, которые называют третьоктавными полосами частот, в каждой третьоктавной полосе выбрана среднегеометрическая частота, по которой ведется измерение уровней звукового давления.
Таблица 2. Среднегеометрические и граничные частоты октавных и третьоктавных полос
| Среднегеометрические частоты Гц | Граничные частоты для полос, Гц (октавных) | Граничные частоты для полос, Гц (третьоктавных) |
|---|---|---|
| 50 | 45-90 | 45-56 |
| 63 | 45-90 | 56-71 |
| 80 | 45-90 | 71-90 |
| 100 | 90–180 | 90–112 |
| 125 | 90–180 | 112–140 |
| 160 | 90–180 | 140–180 |
| 200 | 180–355 | 180–224 |
| 250 | 180–355 | 224–280 |
| 315 | 180–355 | 280–355 |
| 400 | 355–710 | 355–450 |
| 500 | 355–710 | 450–560 |
| 630 | 355–710 | 560–710 |
| 800 | 710–1400 | 710–900 |
| 1000 | 710–1400 | 900–1120 |
| 1250 | 710–1400 | 1120–1400 |
| 1600 | 1400–2800 | 1400–1800 |
| 2000 | 1400–2800 | 1800–2240 |
| 2500 | 1400–2800 | 2240–2800 |
| 3150 | 2800–5600 | 2800–3540 |
| 4000 | 2800–5600 | 3540–4500 |
| 5000 | 2800–5600 | 4500–5600 |
| 6300 | 5600–11200 | 5600–7100 |
| 8000 | 5600–11200 | 7100–9000 |
| 10000 | 5600–11200 | 9000–11200 |
Для измерений уровней звука в реальных условиях используют специальный прибор — шумомер. Так, как чувствительность уха зависит как от частоты, так и от интенсивности звука, поэтому шумомер производит замеры по специальным откорректированным частотным характеристикам A, B, C, D, согласно ГОСТ 17187 обязательной в шумомерах является характеристика А, остальные характеристики являются дополнительными. Таким образом, определение уровня звука в акустике следующее — это энергетическая сумма октавных уровней звукового давления в нормируемом диапазоне частот, откорректированных по частотной характеристике А шумомера по ГОСТ 17187, для её измерения специальная величина дБА.
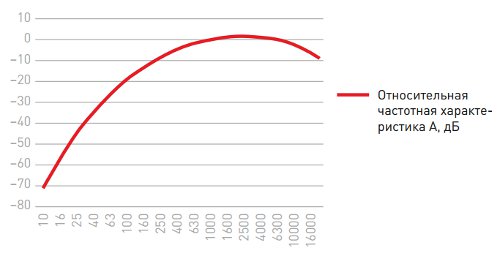
Рисунок 3. Стандартная частотная характеристика "А" шумомера
Таблица 3. Стандартная частотная характеристика "А" шумомера
| Номинальная частота, Гц | 50 | 63 | 80 | 100 | 125 | 160 | 200 | 250 | 315 | 400 | 500 | 630 | 800 | 1000 | 1250 | 1600 | 2000 | 2500 | 3150 | 4000 | 5000 |
| Частотная характеристика "А" шумомера, дБ | 30,2 | 26,2 | 22,5 | 19,1 | 16,1 | 13,4 | 10,9 | 8,6 | 6,6 | 4,8 | 3,2 | 1,9 | 0,8 | 0 | 0,6 | 1 | 1,2 | 1,3 | 1,2 | 1 | 0,5 |